7 algoritmů, které by měl znát každý programátor

Jako student programování jste se během své kariéry pravděpodobně naučili spoustu různých algoritmů. Znalost různých algoritmů je pro každého programátora naprosto zásadní.

S tolika algoritmy může být náročné sledovat, co je podstatné. Pokud se připravujete na pohovor nebo si jen zdokonalujete své dovednosti, tento seznam vám to relativně usnadní. Přečtěte si, jak uvádíme nejdůležitější algoritmy pro programátory.

1. Dijkstraův algoritmus

Edsger Dijkstra byl jedním z nejvlivnějších počítačových vědců své doby a přispěl k tomu mnoho různých oblastí počítačové vědy, včetně operačních systémů, konstrukce kompilátoru a mnoha dalších více. Jedním z nejpozoruhodnějších příspěvků společnosti Dijkstra je vynalézavost jeho algoritmu nejkratších cest pro grafy, známého také jako Dijkstra's Shortest Path Algorithm.

Algoritmus Dijkstra najde jedinou nejkratší cestu v grafu ze zdroje do všech vrcholů grafu. Při každé iteraci algoritmu se přidá vrchol s minimální vzdáleností od zdroje a takový, který v aktuální nejkratší cestě neexistuje. Toto je chamtivá vlastnost, kterou používá Djikstraův algoritmus.

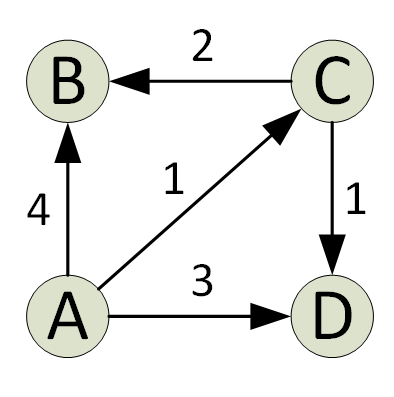
Algoritmus je obvykle implementován pomocí sady. Algoritmus Dijkstra je velmi účinný, když je implementován pomocí Min Heap; nejkratší cestu najdete za pouhých O (V+ElogV) času (V je počet vrcholů a E je počet hran v daném grafu).

Algoritmus Dijkstry má svá omezení; funguje pouze na směrovaných a neorientovaných grafech s hranami kladné váhy. Pro záporné váhy je obvykle vhodnější Bellmanův-Fordův algoritmus.

Otázky k pohovoru běžně zahrnují Djikstraův algoritmus, proto důrazně doporučujeme porozumět jeho složitým detailům a aplikacím.

2. Sloučit třídění

V tomto seznamu máme několik třídicích algoritmů a sloučení je jedním z nejdůležitějších algoritmů. Je to účinný třídicí algoritmus založený na programovací technice Divide and Conquer. V nejhorším případě může sloučení třídit čísla „n“ za pouhých O (nlogn) čas. Ve srovnání s primitivními třídicími technikami, jako je Bubble Sort (což zabere čas O (n^2)), sloučení je mimořádně efektivní.

Příbuzný: Úvod do slučovacího algoritmu řazení

Při sloučení je pole, které má být tříděno, opakovaně rozděleno do podoblastí, dokud se každý dílčí pole skládá z jednoho čísla. Rekurzivní algoritmus pak opakovaně slučuje dílčí pole a třídí pole.

3. Rychlé řazení

Quicksort je další algoritmus řazení založený na programovací technice Divide and Conquer. V tomto algoritmu je nejprve vybrán prvek jako pivot a celé pole je poté rozděleno kolem tohoto pivot.

Jak jste pravděpodobně uhodli, dobrý pivot je pro efektivní třídění klíčový. Pivot může být buď náhodný prvek, mediální prvek, první prvek nebo dokonce poslední prvek.

Implementace quicksortu se často liší ve způsobu, jakým zvolí pivot. V průměrném případě bude quicksort třídit velké pole s dobrým pivotem jen za čas O (nlogn).

Obecný pseudokód rychlého řazení opakovaně rozdělí pole na čepu a umístí jej do správné polohy podoblasti. Také umístí prvky menší než čep vlevo a prvky větší než čep vpravo.

4. Hloubkové první hledání

Depth First Search (DFS) je jedním z prvních grafických algoritmů učených studenty. DFS je účinný algoritmus používaný k procházení nebo prohledávání grafu. Lze jej také upravit tak, aby byl použit při procházení stromů.

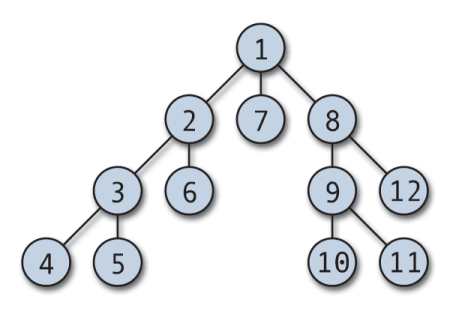
Průchod DFS může začít z libovolného libovolného uzlu a ponoří se do každého sousedního vrcholu. Algoritmus ustupuje, když neexistuje žádný nenavštívený vrchol nebo je slepá ulička. DFS je obvykle implementován se zásobníkem a booleovským polem pro sledování navštívených uzlů. DFS je snadno implementovatelný a výjimečně účinný; funguje (V+E), kde V je počet vrcholů a E je počet hran.

Typické aplikace DFS traversal zahrnují topologické řazení, detekci cyklů v grafu, hledání cesty a hledání silně propojených komponent.

5. Hledání do šířky

Breadth-First Search (BFS) je také známý jako procházení úrovní pro stromy. BFS funguje v O (V+E) podobně jako algoritmus DFS. BFS však místo fronty používá frontu. DFS se ponoří do grafu, zatímco BFS prochází graf po šířce.

Algoritmus BFS využívá frontu ke sledování vrcholů. Navštěvované sousední vrcholy jsou navštíveny, označeny a zařazeny do fronty. Pokud vrchol nemá žádné sousední vrcholy, pak je vrchol odebrán z fronty a prozkoumán.

BFS se běžně používá v sítích peer-to-peer, nejkratší cesta neváženého grafu a k nalezení minimálního překlenovacího stromu.

6. Binární vyhledávání

Binární vyhledávání je jednoduchý algoritmus k nalezení požadovaného prvku v tříděném poli. Funguje to tak, že pole opakovaně rozdělíte na polovinu. Pokud je požadovaný prvek menší než prostřední prvek, bude levá strana prostředního prvku zpracována dále; jinak se pravá strana rozpůlí a znovu se prohledá. Proces se opakuje, dokud není nalezen požadovaný prvek.

Časová složitost binárního vyhledávání je O (logn), což jej činí velmi efektivním při hledání lineárních polí.

7. Minimální algoritmy zahrnující strom

Minimální spanning tree (MST) grafu má minimální náklady mezi všemi možnými spanning stromy. Náklady na klenutý strom závisí na hmotnosti jeho okrajů. Je důležité si uvědomit, že může existovat více než jeden minimální klenutý strom. Existují dva hlavní algoritmy MST, a to Kruskalův a Primův.

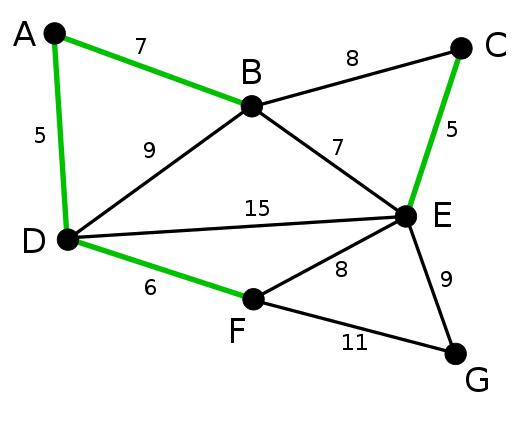
Kruskalův algoritmus vytváří MST přidáním okraje s minimálními náklady do rostoucí sady. Algoritmus nejprve třídí hrany podle jejich hmotnosti a poté přidává hrany k MST počínaje minimem.

Je důležité si uvědomit, že algoritmus nepřidává hrany, které tvoří cyklus. Pro řídké grafy je upřednostňován Kruskalův algoritmus.

Prim’s Algorithm také používá chamtivou vlastnost a je ideální pro husté grafy. Ústřední myšlenkou Primova MST je mít dvě odlišné sady vrcholů; jedna sada obsahuje rostoucí MST, zatímco druhá obsahuje nepoužívané vrcholy. Při každé iteraci je vybrána hrana minimální hmotnosti, která spojí dvě sady.

Algoritmy minimálního spanning stromu jsou zásadní pro klastrovou analýzu, taxonomii a vysílací sítě.

Efektivní programátor ovládá algoritmy

Programátoři se neustále učí a rozvíjejí své dovednosti a existuje několik základních zásad, ve kterých musí být každý zběhlý. Zkušený programátor zná různé algoritmy, výhody a nevýhody každého z nich a který algoritmus by byl pro daný scénář nejvhodnější.

Úvod do algoritmu řazení Shell

I když skořápkové řazení není nejúčinnější metodou, začátečníci si jeho cvičením mohou hodně vydělat.

Číst dále

O autorovi